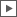Übersicht wichtiger Zahlenkörper/-ringe
| ℕ | ⊊ | ℤ | ⊊ | ℚ | ⊊ | | ℝ ⊊ *ℝ ⊊ surreale Zahlen | ||||||
| ⊊ | ⊊ | | ⊊ | ||||||||||
| ℤ[i] | ⊊ | ℚ(i) | ⊊ | | ℂ := (ℝ2, +, *) = ℝ(i) | ||||||||
| ⊊ | ⊊ | | | ||||||||||
| {α|𝔸} | ⊊ | 𝔸 | ⊊ | | | ||||||||
| ⊊ | ⊊ | ⊊ | | ⊊ | |||||||||
| 𝕂∞,∞ | | | |||||||||||
| ———————————————————————— | |———————————————— | |||||||||||
| ℤ[i,j,k] | ⊊ | ℚ(i,j,k) | ⊊ | | ℍ := (ℝ4, +, *) = ℝ(i,j,k) | ||||||||
| | ⊊ | ||||||||||||
| | 𝕆 := ℝ(i,j,k,l,m,n,o) | ||||||||||||
| | ⊊ | ||||||||||||
| | 𝕊 | ||||||||||||
| ℕ | natürliche Zahlen ⊊ ↓ | kommutativer Bewertungshalbring | D ANBK - ANK | |
| ℤ | ganze Zahlen ⊊ ↓ | 1-dimensional ganz | euklidischer noetherscher Ring | |
| ℤ[i] | gaußsche (ganze) Zahlen ⊊ ↓ | 2-dimensional ganz | D GK - ANK ohne T | |
| {α|𝔸} | ganz algebraische Zahlen | algebraische Zahlen α die ganzes Element über ℤ sind ℤ[α] ist endlich erzeugtes ℤ-Modul |
euklidischer Ganzheitsring | D GK - ANK ohne T |
| ℤ[ω] | Eisenstein-Zahlen | Maximalordnung des quadratischen Zahlkörpers ℚ(√-3) | euklidischer Ganzheitsring | D GK - ANK ohne T |
| positive Brüche ⊊ ↓ | kommutativer Halbkörper | D AK - GK | ||
| positive Brüche mit 0 ⊊ ↓ | kommutativer Halbkörper mit 0 | D ANBK - GK | ||
| ℚ | rationale Zahlen ⊊ ↓ | 1-dimensional rational | geordneter Körper | D GK - GK |
| ℚ(i) | gaußsche rationale Zahlen | 2-dimensional rational | Kreisteilungskörper, imaginärquadratischer Zahlkörper | D GK - GK |
| konstruierbare Zahlen ⊊ ↓ | mit Zirkel und Lineal konstruierbar euklidischer Abschluss von ℚ |
archimedisch geordneter euklidischer Körper | D GK - GK | |
| reell abgeschlossener archimedisch geordneter euklidischer Körper | D GK - GK | |||
| 𝔸 | algebraische Zahlen ⊊ ↓ | algebraische Erweiterung von ℚ, deg(𝔸 : ℚ) = ℵ0 |
algebraisch abgeschlossener pythagoreischer Körper | D GK - GK |
| 𝕂∞,∞ | konstruktive Zahlen | mit drei Klammern (-, e, ln) konstruierte verschachtelte Baumstrukturen, trdeg(𝕂∞,∞ : ℚ) = ℵ0 𝕂0,0 = 𝔸, 𝕂0,1 = 𝔸({ln k | k ∈ 𝔸\0}), 𝕂1,0 = 𝔸({ek | k ∈ 𝔸}), 𝕂1,1 = 𝕂1,0({ln k | k ∈ 𝕂1,0\0}) = 𝕂0,1({ek | k ∈ 𝕂0,1}), ... trdeg(𝕂n+1,m : 𝕂n,m) = trdeg(𝕂n,m+1 : 𝕂n,m) = ℵ0 ? |
algebraisch abgeschlossene pythagoreische Körper | D GK - GK |
| ———————————————— überabzählbar unendlich —————————————————— | ||||
| proendliche Zahlen | Rest in allen ganzzahligen Restklassenringen | proendliche Gruppe -- kompakt, total unzusammenhängend | G | |
| ℤp | ganze p-adische Zahlen ⊊ ↓ | Folge von Restklassen aus ℤ/pnℤ | diskreter Bewertungsring und proendliche Gruppe -- wie oben + vollständig | D GK - ANK ohne T |
| ℚp | p-adische Zahlen ⊊ ↓ | {p-n | n ∈ ℕ0} • ℤp= ℚ • ℤp = ℚ + ℤp | nicht geordneter Körper -vollständig, lokalkompakt, total unzusammenhängend | D GK - GK |
| ℂp | Vervollständigung des algebraischen Abschlusses der Metrik auf ℚp | algebraisch abgeschlossener nicht geordneter Körper | D GK - GK | |
| ℝ | reelle Zahlen ⊊ ↓ | 1-dimensional reell - am wenigsten mächtiges konsistent behauptbares Kontinuum |
reell abgeschlossener archimedisch geordneter euklidischer Körper | D GK - GK |
| ℂ | komplexe Zahlen | 2-dimensional reell ℂ = ℝ(i) | algebraisch abgeschlossener pythagoreischer Körper | D GK - GK |
| *ℝ | hyperreelle Zahlen | Folgen von reellen Zahlen | reell abgeschlossener Körper | D GK - GK |
| ℵOn | Kardinalzahlen | Mächtigkeit einer Menge | echte Klasse mit Eigenschaften eines kommutativen Bewertungshalbrings | D ANBK - ANK |
| Kardinalzahlen bis zu einer oberen Schranke | kommutativer Bewertungshalbring | D ANBK - ANK | ||
| zusätzlich beschränkt auf unendliche Kardinalzahlen und 0 und 1 | kommutatives Dioid | D ANBKP - ANKP | ||
| On | Ordinalzahlen ⊊ ↓ | Position in einer geordneten Menge | echte Klasse mit Monoideigenschaften | D AN - AN |
| surreale Zahlen ⊊ ↓ | Äquivalenzklassen von konstruierten Mengen | echte Klasse mit Eigenschaften eines geordneten Körpers | D GK - GK | |
| —————————————————————————————————————— hyperkomplex —————————————————————————————————————————————————— | ||||
| ℤ[i,j,k] | Hurwitzquaternion | 4-dimensional ganz | euklidischer Ganzheitsring | D GK - ANK ohne T |
| ℚ(i,j,k) | rationale Quaternionen | 4-dimensional rational | Schiefkörper (Divisionsring) | D GK - G |
| berechenbare Zahlen | berechenbar durch eine Turingmaschine | Körper | D GK - GK | |
| ———————————————— überabzählbar unendlich —————————————————— | ||||
| ℍ | Quaternionen ⊊ ↓ | 4-dimensional reell | Schiefkörper (Divisionsring) | D GK - G |
| 𝕆 | Oktonionen ⊊ ↓ | 8-dimensional reell | Alternativkörper | D GK - AltNI |
| 𝕊 | Sedenionen | 16-dimensional reell | nichtkommutative Jordan-Algebra | D GK - FlexNI |
| ———————————————————————————————————————————————————————————————————————————————————————————————— | ||||
| definierbare Zahlen | definiert in einer formalen Sprache | ? | ||
konstruktive Zahlen
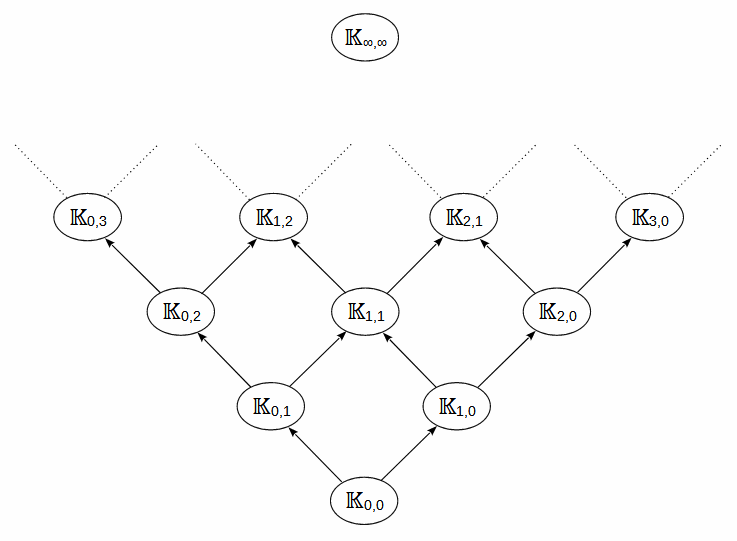
unendlicher distributiver Verband transzendenter Erweiterungskörper
hyperkomplex Zahlen
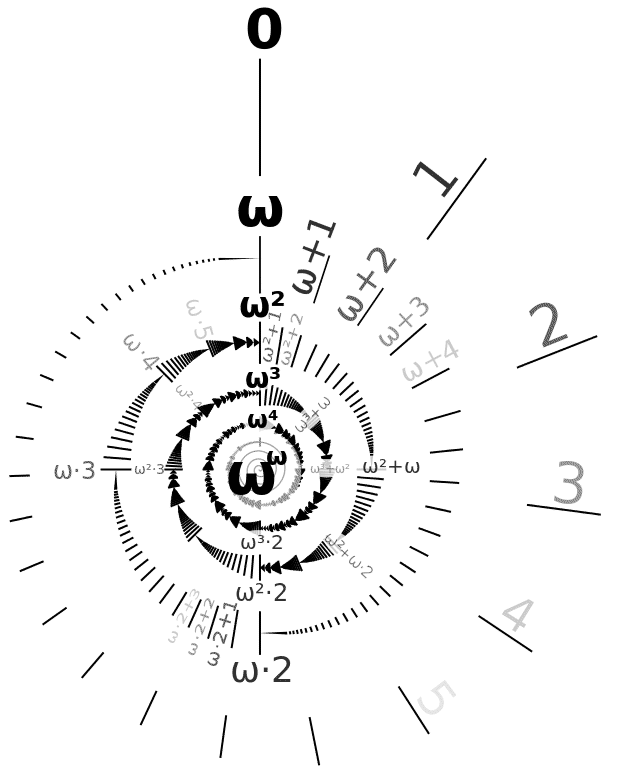
Ordinalzahlen
transitive Menge - x ∈ y ∧ y ∈ M → x ∈ M bzw. x ∈ M → x ⊂ M bzw. M ⊂ P(M)
Ordinalzahl - transitive Menge aus Ordinalzahlen (nach Neumann-Zermelo)
jede wohlgeordnete Menge ist ordnungsisomorph zu genau einer Ordinalzahl
z.B. ist {0, 2, 4, 6, ..., ω, ω + 2, ω + 4, ω + 6} ordnungsisomorph zu {0, 1, 2, 3, ..., ω, ω + 1, ω + 2, ω + 3}
0 = ∅
1 = {∅}
2 = {∅, {∅}}
3 = {∅, {∅}, {∅,{∅}}}
4 = {∅, {∅}, {∅,{∅}}, {∅,{∅},{∅,{∅}}}}
5 = {∅, {∅}, {∅,{∅}}, {∅,{∅},{∅,{∅}}}, {∅, {∅}, {∅,{∅}}, {∅,{∅},{∅,{∅}}}}}
...
ω = ω0 = {0, 1, 2, ...} = {∅, {∅}, {∅,{∅}}, ...} - erste bzw. kleinste (abzählbar) unendliche Ordinalzahl bzw. Limes-Ordinalzahl
ω + 1 = {0, 1, 2, ..., {0, 1, 2, ...}} = {0, 1, 2, ..., ω} = {∅, {∅}, {∅,{∅}}, ..., {∅, {∅}, {∅,{∅}}, ...}}
ω + 2 = {0, 1, 2, ..., {0, 1, 2, ...}, {0, 1, 2, ..., {0, 1, 2, ...}}} = {0, 1, 2, ..., ω, ω + 1}
...
ω * 2 = {0, 1, 2, ..., {0, 1, 2, ...}, {0, 1, 2, ..., {0, 1, 2, ...}}, ...} = {0, 1, 2, ..., ω, {0, 1, 2, ..., ω}, ...} = {0, 1, 2, ..., ω, ω + 1, ...}
ω * 2 + 1 = {0, 1, 2, ..., {0, 1, 2, ...}, {0, 1, 2, ..., {0, 1, 2, ...}}, ..., {0, 1, 2, ..., {0, 1, 2, ...}, {0, 1, 2, ..., {0, 1, 2, ...}}, ...}}
ω * 2 + 2 = {0, 1, 2, ..., ω, ω + 1, ..., {0, 1, 2, ..., ω, ω + 1, ...}, {0, 1, 2, ..., ω, ω + 1, ..., {0, 1, 2, ..., ω, ω + 1, ...}}}
...
ω * 3 = {0, 1, 2, ..., ω, ω + 1, ..., {0, 1, 2, ..., ω, ω + 1, ...}, {0, 1, 2, ..., ω, ω + 1, ..., {0, 1, 2, ..., ω, ω + 1, ...}}, ...}
...
ω * 4 = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...}
...
ω2 = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2}
ω2 + 1 = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2}
...
ω2 + ω = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2, ω2 + 1, ...}
...
ω2 * 2 = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2, ω2 + 1, ..., ω2 + ω, ω2 + ω + 1, ..., ω2 + ω * 2, ...2}
...
ω3 = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2, ω2 + 1, ..., ω2 + ω, ω2 + ω + 1, ..., ω2 + ω * 2, ...3}
...
ωω = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2, ω2 + 1, ..., ω2 + ω, ω2 + ω + 1, ..., ω2 + ω * 2, ...ω}
...
ωωω = {0, 1, 2, ..., ω, ω + 1, ..., ω * 2, ω * 2 + 1, ..., ω * 3, ω * 3 + 1, ...2, ω2, ω2 + 1, ..., ω2 + ω, ω2 + ω + 1, ..., ω2 + ω * 2, ...ωω}
...
ωωωω... = ε0 = ωε0 - erste Ordinalzahl mit Fixpunkteigenschaft
ε0 + 1
ε0 + ω
ε0 + ω2
ε0 + ωω
ε0 * 2
ε02
ε0ω
ε0ωω
ε0ωωω... = ε0ε0
ε0ε0 + 1
...
ε0ε0ε0... = ε1 = ε0ε1 = ωε0ε1 = ωε1 - zweite Ordinalzahl mit Fixpunkteigenschaft
ε1 + 1
...
ε1ε1ε1... = ε2 = ε1ε2 = ωε1ε2 = ωε2 - dritte Ordinalzahl mit Fixpunkteigenschaft
ε2 + 1
...
εω = ωεω - ω-te Ordinalzahl mit Fixpunkteigenschaft
εω + 1
...
εω+1
εω*2
εω2
εωω
εωωω... = εε0
εε0 + 1
...
εεε... = ω1 = εω1 - Ordinalzahl mit 2. Fixpunkteigenschaft - erste bzw. kleinste überabzählbar unendliche Ordinalzahl - Mächtigkeit von ℝ
ω1 + 1
...
ω1ω1ω1... = π0 = ω1π0 - erste Ordinalzahl mit 3. Fixpunkteigenschaft
π0 + 1
...
π0π0π0... = π1 = π0π1 = ω1π1 - zweite Ordinalzahl mit 3. Fixpunkteigenschaft
π1 + 1
...
πππ... = ω2 = πω2 - Ordinalzahl mit 4. Fixpunkteigenschaft - erste bzw. kleinste überüberabzählbar unendliche Ordinalzahl
ω2 + 1
...
ωω - Ordinalzahl mit 2*ω. Fixpunkteigenschaft - erste bzw. kleinste ω-fach überabzählbar unendliche Ordinalzahl
ωω + 1
...
ωωω - erste bzw. kleinste ωω -fach überabzählbar unendliche Ordinalzahl
ωωω + 1
...
ωωωω... - Wie soll man so was noch bezeichnen?
ωωωω... + 1
...
Ω = Ω + 1 - größte Ordinalzahl - unendlichvielfältig unendlichfach gesteigerte Unendlichkeit - nicht konsistent definierbar bzw. formalisierbar (ebenso wie Gott Typ 1, Welt und Leben)
Kardinalzahlen
0 = 0 = ∅
1 = 1 = {∅}
2 = 2 = {∅, {∅}}
3 = 3 = {∅, {∅}, {∅,{∅}}}
4 = 4 = {∅, {∅}, {∅,{∅}}, {∅,{∅},{∅,{∅}}}}
...
ℵ0 = ℶ0 = |ω| = |ℕ| - abzählbar unendliche Mächtigkeit - Mächtigkeit von ℕ
unter Voraussetzung des Auswahlaxiom gilt ω = ℵ0 = ℶ0 bzw. ℵ ⊊ On wodurch Kardinalzahlen zu speziellen (Neumann-Zermelo-)Ordinalzahlen und somit zu (wohlgeordneten) Mengen werden
ℵ1 ≤ ℶ1 = ω1 = 2ℵ0 = 2|ℕ| = |ℝ| - überabzählbar unendliche Mächtigkeiten - Mächtigkeit von ℝ
für alle Ordinalzahlen a > 0 gilt ωa = ℶa und ℵa ≤ ℶa und ℵa+1 ≤ 2ℵa
| unter Voraussetzung der Kontinuumshypothese (CH) gilt | 2ℵa = ℵa+1 | ℵa = ℶa | ℵ1 = ℶ1 = ω1 = |ℝ| = 2|ℕ| < ℵ2 = ℶ2 = ω2 = 2|ℝ| < ... |
| unter Voraussetzung der Negation von CH gilt | 2ℵa > ℵa+1 | ℵa < ℶa | ℵ1 < ℶ1 = ω1 = |ℝ| = 2|ℕ| < ℶ2 = ω2 = 2|ℝ| < ... |