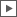Konstruktive Zahlen
Das, was ich hier als konstruktive Zahlen vorstellen möchte, basiert auf einem Kalkül von Jeffrey M. James, das er in seiner Masterarbeit "A Calculus of Number Based on Spatial Forms" von 1993 vorgestellt hatte. Diese wiederum baut auf Ideen von John Horton Conway, George Spencer-Brown, Louis H. Kauffman und William Bricken auf. Das Kalkül von James erzeugt mit lediglich drei verschiedenen Klammern ausgehend von drei einfachen Axiomen einen sehr mächtigen Zahlenkörper mit vielen interessanten Eigenschaften. Es ist mit der minimalistischen Notation ohne jeglichen syntaktischen Zucker zwar nicht praktikabel, eine Buchhaltung zu betreiben, dafür werden Rechenregeln und -gesetze auf eine anschauliche und fast schon meditative Art und Weise sichtbar gemacht.
Das Kalkül verwendet drei verschiedene Klammern. Eine runde für die e-Funktion, eine eckige für den natürlichen Logarithmus ln(x) und eine spitze für die Inversion. Die damit konstruierten verschachtelten Baumstrukturen verwenden den Zeichenhintergrund gewissermaßen als leeren Raum, der durch ihre Grenzziehungen eine Struktur erhält. Da e0 gleich 1 ist, erhält man, wenn man ausschließlich runde Klammern für die e-Funktion zulässt, und nicht gestattet die Klammern zu verschachteln, ein Kalkül für die natürlichen Zahlen. Gestattet man zusätzlich spitze Klammern für die Inversion, welche mit den runden Klammern verschachtelt werden dürfen, erhält man die ganzen Zahlen. Zusammen mit eckigen Klammern für den natürlichen Logarithmus, welche aber nur abwechselnd mit den runden Klammern in diese verschachtelt werden dürfen, wobei für die spitzen Klammern weiterhin keine Einschränkungen existieren, ergeben sich die rationalen Zahlen. Man könnte diese auch als beliebig verschachtelte Multiplikationen und Inversionen von ganzen Zahlen beschreiben. Gestattet man zusätzlich Exponentiationen mit beliebig verschachtelten Basen und rationalen Exponenten, ergeben sich die algebraischen Zahlen.
Gibt man, mit Ausnahme von ln(0) mit wiederum zwei Einschränkungen, sämtliche Verschachtelungsmöglichkeiten frei, so erhält man einen unendlichen distributiven Verband transzendenter Erweiterungskörper mit jeweils abzählbar unendlichem Transzendenzgrad.
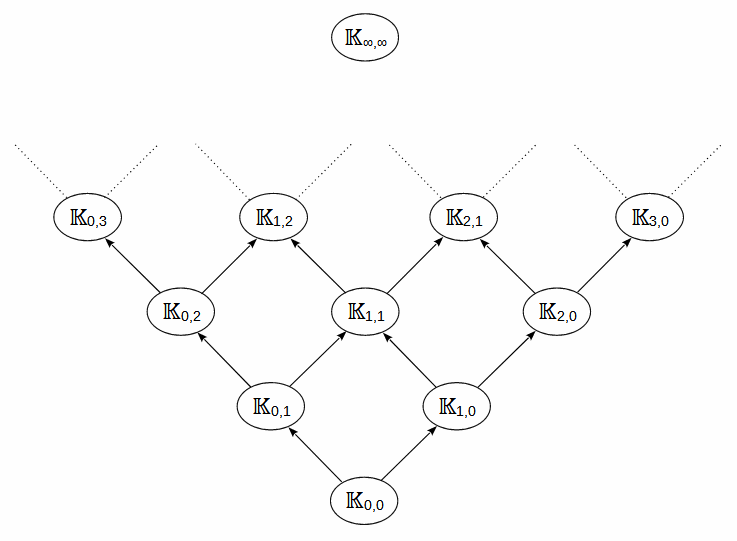
𝕂0,0 = 𝔸
𝕂0,1 = 𝔸({ln k | k ∈ 𝔸\0})
𝕂1,0 = 𝔸({ek | k ∈ 𝔸})
𝕂0,2 = 𝕂0,1({ln k | k ∈ 𝕂0,1\0})
𝕂1,1 = 𝕂0,1({ek | k ∈ 𝕂0,1}) = 𝕂1,0({ln k | k ∈ 𝕂1,0\0})
𝕂2,0 = 𝕂1,0({ek | k ∈ 𝕂1,0})
...
𝕂n,m+1 = 𝕂n,m({ln k | k ∈ 𝕂n,m\0})
𝕂n+1,m = 𝕂n,m({ek | k ∈ 𝕂n,m})
...
𝕂∞,∞
Der kleinste Körper des Verbandes 𝕂0,0 ist gleich den algebraischen Zahlen und der größte ist 𝕂∞,∞.
In ihm können e-Funktionen und natürliche Logarithmen potenziell unendlich oft ineinander verschachtelt werden.
e wäre Element in allen Körpern die mindestens 𝕂1,0 enthalten
und ee in allen ab 𝕂2,0.
π wäre Element in allen Körpern die mindestens 𝕂0,1 enthalten,
ln(π) in allen ab 𝕂0,2
und eπ in allen ab 𝕂1,1.
Es gibt bis heute noch keinen Beweis, dass e und π algebraisch unabhängig sind, auch wenn es sehr stark danach aussieht. Insofern ist noch nicht bewiesen, dass alle Erweiterungskörper einen abzählbar unendlichem Transzendenzgrad besitzen. Alle Körper des Verbandes besitzen eine abzählbar unendliche Mächtigkeit, da ein einfacher Algorithmus iterativ sämtliche Elemente konstruieren könnte. Aufgrund dessen wäre mein Vorschlag, die Zahlenkörper als konstruktive Zahlen zu benennen. Reelle Zahlen sind diesen gegenüber überabzählbar unendlich. Somit gibt es reelle Zahlen, welche außerhalb von 𝕂∞,∞ liegen. Diese könnte man als destruktive Zahlen bezeichnen. Es ist jedoch bereits schwierig die Irrationalität oder Transzendenz bestimmter Zahlen zu beweisen. Wahrscheinlich ist der Beweise der Destruktivität von Zahlen noch schwieriger, auch wenn durch die iterative Konstruierbarkeit eine neue Form induktiver Beweise möglich wird. Die erste Zahl, für die 1844 der Beweis ihrer Transzendenz gelang, ist eine Liouvillesche Zahl. Nach meinem Gefühl ist sie ein heißer Kandidat für eine Zahl, die nicht nur transzendent sondern sogar destruktiv ist.
f1(x) = x f2(x) = -x f3(x) = ex f4(x) = ln x f3(f4(x)) = x eln x = x f4(f3(x)) = x ln ex = x <> - Inversion -0 = 0 () = o - Instanzierung e0 = 1 [] = ∎ - Abstraktion ln 0 = -∞ + [-∞...∞]i (vollständige Mehrdeutigkeit im Imaginärteil) [(a)] = ([a]) = a Abbau Axiom 1 ln ea = eln a = a (a[bc]) = (a[b])(a[c]) Distribution von a Axiom 2 ea + ln (b + c) = ea + ln b + ea + ln c a<a> = Inversion von a Axiom 3 a - a = 0 <<a>> = a Inversionsaufhebung (doppelte Inversion) Theorem 1 -(-a) = a <a><b> = <ab> Inversionszusammenfassung Theorem 2 (-a) + (-b) = -(a + b) Beweis der Inversionsaufhebung <<a>> <<a>><a>a -Inversion von a a Inversion von <a> Beweis der Inversionszusammenfassung <a><b> <a><b>ab<ab> -Inversion von ab <ab> Inversion von a und b Beweis der additiven Selbstinversheit des leeren Raumes -0 = 0 <> Inversion von Kardinalität von a (Aggregation zweiten Grades) a = ([a]) = ([a][o]) -Abbau2, -Abbau1 aa = ([a][o])([a][o]) = ([a][oo]) 2x a, -Distribution von [a] a...n = ([a][o...n]) Induktionsschritt über n ∈ ℕ a * b => ([a][b]) a / b => ([a]<[b]>) für b != Beweis der Assoziativität der Multiplikation (a*b)*c = a*(b*c) ([([a] [b])][c] ) ( [a] [b] [c] ) Abbau1 ( [a][([b] [c])]) -Abbau1 Beweis der multiplikativen Selbstinversheit von o 1/1 = 1 (<[o]>) (< >) Abbau1 ( ) Inversion von
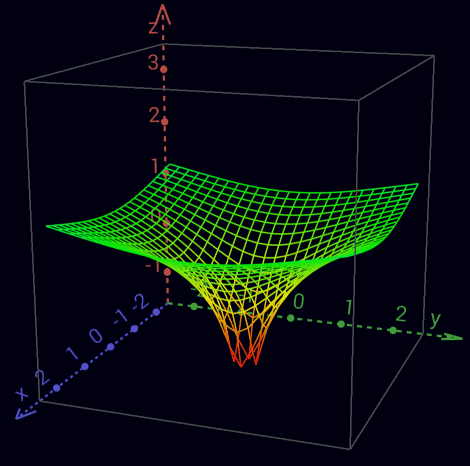
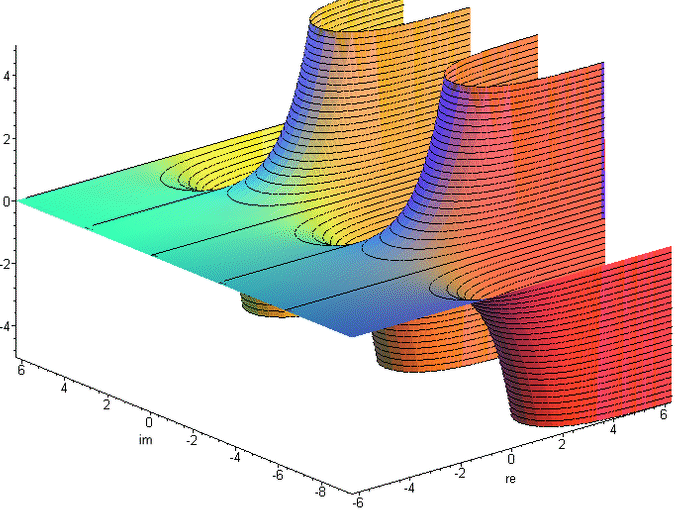
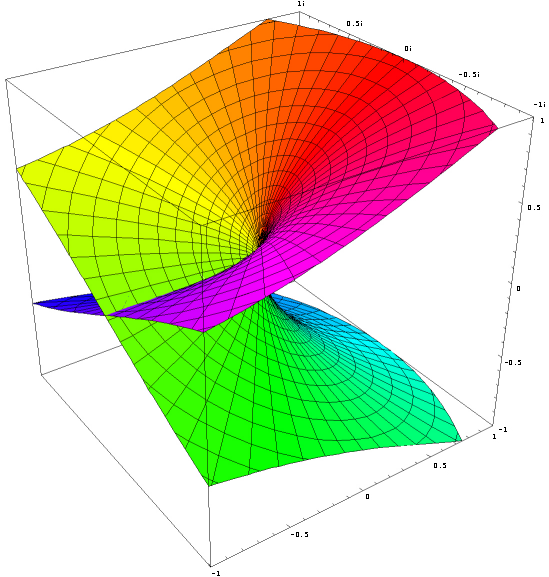
Realteil des komplexen Logarithmus
Imaginärteil des komplexen Logarithmus - Riemannsche Fläche Absorbtion ([a]∎) = Null-Kardinalität von a Theorem 3 a * 0 = 0 Beweis der Null-Kardinalität von a ([a]∎) ([a]∎)([a][b])<([a][b])> -Inversion von ([a][b]) ([a][b])<([a][b])> -Distribution von [a] Inversion von ([a][b]) Unbestimmtheit der Kardinalität von ∎ innerhalb von () 0 = eln 0 = 0 * 0 = 0 * 0 * 0 = ... = (∎) = (∎∎) = (∎∎∎) = (∎∎∎∎) = ... -Abbau2, -Null-Kardinalität von = <> = [o] = (∎) = [(<>)] = ([<>]) = <[o]> = <(∎)> 3x Abbau1, 3x Abbau2, 5x Inversion von Undefiniertheit der Inversion von ∎ innerhalb von () (<∎>) = ([o]<∎>) <= 1/0 ist undefiniert (Singularität) 0 * ? = 1 Null hat kein multiplikatives Inverses 0/0 mehrdeutig 0/a = 0 a/a = 1 a/0 = ∞ Kardinalität von [a] (Aggregation dritten Grades) ([a]...[a]) = (([[a]][o...o])) (([[a]][b])) ab Aufgrund der vollständigen Mehrdeutigkeit im Imaginärteil von ln 0 ist ∎ neben der Null-Kardinalität nur noch bei einer 0-Basis definiert. 0n = 0 n ∈ ℕ \ 0 (([∎][o...n])) ( ∎...n ) Kardinalität von ∎ ( ∎ ) Unbestimmtheit der Kardinalität von ∎ Abbau2 0q = 0 q ∈ ℚ \ 0 (( [∎][ q ])) (( [∎][([m] <[n]>)])) m, n ∈ ℕ \ 0 (( [∎] [m] <[n]> )) Abbau1 (([[(([∎] [m]))]]<[n]> )) 2x -Abbau1 (([[ ]]<[n]> )) 0m = 0 (( [∎] <[n]> )) Unbestimmtheit der Kardinalität von ∎ (( [∎] [(<[n]>)])) -Abbau1 Null-Kardinalität von (<[n]>) 00 = 1 (([∎]∎)) ( ) Null-Kardinalität von ∎ a0 = 1 (([[a]]∎)) ( ) Null-Kardinalität von [a] a1 = a (([[a]][o])) (([[a]] )) Abbau1 a 2x Abbau2 Da die Multiplikation ebenso kommutativ ist wie die Addition, können Faktoren ebenso aggregiert werden wie Summanden. Addition 2 + 4 = 6 Multiplikation 2 * 4 = 2 + 2 + 2 + 2 = 8 Exponentiation 24 = 2 * 2 * 2 * 2 = 16 Tetration 42 = 2222 = 224 = 216 = 65.536 Hyper-5 24 = 2222 = 422 = 65.5362 = 2...2 65.536 mal - dafür ist unser Universum erheblich zu klein ... Da die Exponentiation nicht kommutativ ist, können Exponenten nicht aggregiert dargestellt werden wie Summanden oder Faktoren. Dadurch verlieren Aggregationen ab hier gewissermaßen ihre Schönheit und somit ihre Nützlichkeit. oo ooo 2 + 3 = 5 ( [oo] [ooo] ) = oo oo oo 2 * 3 = 2 + 2 + 2 = 6 (([[oo]] [ooo])) = ([oo] [oo] [oo]) 23 = 2 * 2 * 2 = 8 (([[oo]][ (([[oo]][oo])) ])) 32 = 222 = 16 (([[oo]][ (([[oo]][ (([[oo]][oo])) ])) ])) 23 = 222 = 42 = 2222 = 65.536 ... 2+2 = 2*2 = 22 = 22 = 22 = ... = 4 Inversion ( [<a>]b ) = <( [a]b )> Inversionsbeförderung1 Theorem 4 -a * eb = -(a * eb) (<[<a>]b>c) = <(<[a]b>c)> Inversionsbeförderung2 Theorem 5 1/(-a * eb) * ec = -(1/(a * eb) * ec) Beweis der Inversionsbeförderung1 ([<a>]b) <([a]b)>([a]b)([<a>]b) -Inversion von ([a]b) <([a]b)>([a <a>]b) -Distribution von b <([a]b)>([ ]b) Inversion von a <([a]b)>([ ] ) Null-Kardinalität von (b) <([a]b)> Abbau2 Beweis der Inversionsbeförderung2 (c<b [<a>]> ) (c<b [<a>]><[<d>] >[<d>]) -Inversion von [<d>] <(c<b [<a>]><[<d>] >[ d ])> Inversionsbeförderung1 <(c<b [<a>] [<d>] >[ d ])> Inversionszusammenfassung <(c<b[ ([<a>] [<d>]) ]>[ d ])> -Abbau1 <(c<b[<<([ a ] [ d ])>>]>[ d ])> 2x Inversionsbeförderung1 <(c<b[ ([ a ] [ d ]) ]>[ d ])> Inversionsaufhebung <(c<b [ a ] [ d ] >[ d ])> Abbau1 <(c<b [ a ]><[ d ] >[ d ])> -Inversionszusammenfassung <(c<b [ a ]> )> Inversion von [d] Operatoren -a => <a> a+b => ab a+b+c => abc a-b => a<b> a*b => ([a][b]) a*b*c => ([a][b][c]) a*-b => ([a][<b>]) = <([a][b])> = ([<a>][b]) +-Inversionsbeförderung1 a/b => ([a]<[b]>) für b != 1/b => ([o]<[b]>) = (<[b]>) Abbau1 für b != a/a => ([a]<[a]>) = o Inversion von [a] für a != ab => (([[a]][b])) a1 => (([[a]][o])) = (([[a]])) = a Abbau1, 2x Abbau2 a-b => (([[a]][<b>])) a1/b => (([[a]]<[b]>)) = (([[a]][(<[b]>)])) -Abbau1 für b != ac/b => (([[a]]<[b]>[c])) = (([[a]][(<[b]>[c])])) -Abbau1 für b != abc (([[a]][(([[b]][c]))])) (([[a]] ([[b]][c]) )) Abbau1 ((ab)c)1/d = ab * c / d (([[(([[(([[a]][b]))]][c]))]]<[d]>)) (( [[a]][b] [c] <[d]>)) 4x Abbau1 (1/a)b = a-b ( ([[(<[a]>)]][ b ]) ) ( ([ <[a]> ][ b ]) ) Abbau1 (<([ [a] ][ b ])>) Inversionsbeförderung1 ( ([ [a] ][<b>]) ) -Inversionsbeförderung1 ab * ac = ab + c ([(([[a]][b]))][(([[a]][c]))]) ( ([[a]][b]) ([[a]][c]) ) 2x Abbau1 ( ([[a]][b c]) ) Distribution von [[a]] ac * bc = (a * b)c ([(([[a]][c]))] [(([[b]][c]))]) ( ([[a]][c]) ([[b]][c]) ) 2x Abbau1 ( ([[a] [b]][c]) ) Distribution von [c] 1 / e = e-1 ([o]<[(o)]>) ( <[(o)]>) ( < o >) 2x Abbau1 1 / e2 = e-2 ([o]<[(oo)]>) ( <[(oo)]>) ( < oo >) 2x Abbau1 ln (a * b) = ln a + ln b [([a][b])] [a][b] Abbau1 ln (a / b) = ln a - ln b [([a]<[b]>)] [a]<[b]> Abbau1 ln (ab) = ln a * b [(([[a]][b]))] ([[a]][b]) Abbau1 logb a = ln a/ln b ([[a]]<[[b]]>) 1/(1/a) = a (<[(<[a]>)]>) (< <[a]> >) Abbau1 ( [a] ) Inversionsaufhebung a Abbau2 (1/a)*(1/b) = 1/(a*b) ([(< [a]>)][(<[b] >)]) ( < [a]> <[b] > ) 2x Abbau1 ( < [a] [b] > ) Inversionszusammenfassung ( <[([a] [b])]> ) -Abbau1 a/c + b/d = (a*d + b*c) / c*d ( [a] <[c]>)( [b] <[d]>) ( [a][d] <[d]><[c]>)( [b][c] <[c]><[d]>) -Inversion von [d] und [c] ( [a][d] <[d] [c]>)( [b][c] <[c] [d]>) 2x Inversionszusammenfassung ([([a][d])]<[d] [c]>)([([b][c])]<[c] [d]>) 2x -Abbau1 ([([a][d]) ([b][c])]<[c] [d]>) -Distribution von <[c][d]> 1/a + 1/b = (a + b) / a*b ( <[a]>)( <[b]>) ([b]<[b]><[a]>)([a]<[a]><[b]>) -Inversion von [b] und [a] ([b]<[b] [a]>)([a]<[a] [b]>) 2x Inversionszusammenfassung ([b a]<[a] [b]>) -Distribution von <[a][b]> (a + b) * (a - b) = a² - b² ([a b][a <b>]) ([a b][a]) ([a b][<b>]) Distribution von [ab] ([a][a])([b][a]) ([a][<b>]) ([b][<b>]) Distribution von [a] und [<b>] ([a][a])([b][a])<([a][ b ])><([b][ b ])> 2x -Inversionsbeförderung1 ([a][a]) <([b][ b ])> Inversion von ([a][b]) (([[a]][oo])) <(([[b]][oo]))> Kardinalität von [a] und [b] Nummern 0 => 1 => o 2 => oo -1 => <o> -2 => <oo> 1/2 => (<[oo]>) 2/3 => ([oo]<[ooo]>) 43 => ([b][oooo])ooo für b = oooooooooo 243 => ([b][([b][oo])oooo])ooo für b = oooooooooo 1243 => ([b][([b][boo])oooo])ooo für b = oooooooooo Stelligkeit {a} = ([oooooooooo][a]) Definition von {} oooooooooo{a} = {o a} Übertrag+ Kardinalität von oooooooooo {a}{b} = {ab} Zusammenfassung+ ([{a}]b) = {([a]b)} Beförderung+ {} = Null-Kardinalität+ 23 * 114 = 2622 ([ {oo}ooo ] [ {{o}o}oooo ]) ([{oo}][{{o}o}oooo]) ([ooo][{{o}o}oooo]) Distribution von [{{o}o}oooo] {([ oo ][{{o}o}oooo])} ([ooo][{{o}o}oooo]) Beförderung+ {{{o}o}oooo{{o}o}oooo} {{o}o}oooo{{o}o}oooo{{o}o}oooo 2x -Kardinalität von {{o}o}oooo {{{o}o}oooo{{o}o}oooo} {{o}o}{{o}o}{{o}o}oooooooooooo Zusammenfassung+ von o {{{o}o}oooo{{o}o}oooo} {{o}o}{{o}o}{{o}oo} oo Übertrag+ {{{o}o} {{o}o} {o}{o}{o} oooooooooooo} oo Zusammenfassung+ von {o} {{{o}o} {{o}o} {o}{o}{oo} oo} oo Übertrag+ {{{o} {o} oooooo} oo} oo Zusammenfassung+ von {{o}} {{{ oo} oooooo} oo} oo Zusammenfassung+ von {{{o}}} Inverse Stelligkeit /a\ = (<[oooooooooo]>[a]) Definition von /\ /oooooooooo a\ = o/a\ Übertrag- Kardinalität von oooooooooo /a\/b\ = /ab\ Zusammenfassung- ([/a\]b) = /([a]b)\ Beförderung- /\ = Null-Kardinalität- {/a\} = /{a}\ = a Stelligkeitsaufhebung 12,1 * 1,012 = 12,2452 ([ {o}oo/o\ ] [ o//o/oo\\\ ]) ([{o}][o//o/oo\\\]) ([oo][o//o/oo\\\]) ([/o\][o//o/oo\\\]) 2x Distribution von [o//o/oo\\\] {([ o ][o//o/oo\\\])}([oo][o//o/oo\\\])/([ o ][o//o/oo\\\])\ 2x Beförderung ± { o//o/oo\\\ } o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ 3x -Kardinalität von o//o/oo\\\ {o}{ //o/oo\\\ } o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ -Zusammenfassung+ {o} /o/oo\\ o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ Stelligkeitsaufhebung1 {o}oo /o/oo\\ //o/oo\\\ //o/oo\\\ /o//o/oo\\\ \ Zusammenfassung+ von o {o}oo /oo/oo\ /o/oo\\ /o/oo\\ //o/oo\\\ \ Zusammenfassung- of /o\ {o}oo /oo/oooo /oo\ /oo\ /o/oo\\\ \ Zusammenfassung- of //o\\ {o}oo /oo/oooo /ooooo /oo\\\ \ Zusammenfassung- of ///o\\\ 100 / 3 = 33,3... ([ {{o}} ]<[ooo]>) {([ {o} ]<[ooo]>)} Beförderung+ {([oooooooooo]<[ooo]>)} -Übertrag+ {([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>) ([o]<[ooo]>)} 3x Distribution von <[ooo]> {( )( )( ) ([o]<[ooo]>)} 3x Inversion von [ooo] {ooo} {([o]<[ooo]>)} -Zusammenfassung+ {ooo} ([{o}]<[ooo]>) -Beförderung+ {ooo} ([oooooooooo]<[ooo]>) -Übertrag+ {ooo}([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>) ([o]<[ooo]>) 3x Distribution von <[ooo]> {ooo}( )( )( ) ([o]<[ooo]>) 3x Inversion von [ooo] {ooo}ooo ([/oooooooooo\]<[ooo]>) -Übertrag- {ooo}ooo /([ oooooooooo ]<[ooo]>) \ Beförderung- {ooo}ooo/([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>)([o]<[ooo]>) \ 3x Distribution von <[ooo]> {ooo}ooo/( )( )( )([o]<[ooo]>) \ 3x Inversion von [ooo] {ooo}ooo/ooo ([/oooooooooo\]<[ooo]>) \ -Übertrag- {ooo}ooo/ooo /([ oooooooooo ]<[ooo]>)\\ Beförderung- ... 100 / 3,3 = 30,3030... ([ {{o}} ]<[ooo/ooo\]>) {([ {o} ]<[ooo/ooo\]>)} Beförderung+ {([oooooooooo]<[ooo/ooo\]>)} -Übertrag+ {([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>)} -Übertrag- und 3x -Zusammenfassung- {([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito) ([ /o\ ]<[ooo/ooo\]>)} 3x Distribution von <[ooo/ooo\]> {( )( )( ) ([ /o\ ]<[ooo/ooo\]>)} 3x Inversion von [ooo/ooo\] {ooo} {([ /o\ ]<[ooo/ooo\]>)} -Zusammenfassung+ {ooo} ([{/o\}]<[ooo/ooo\]>) -Beförderung+ {ooo} ([ o ]<[ooo/ooo\]>) Stelligkeitsaufhebung1 {ooo} ([/oooooooooo\]<[ooo/ooo\]>) -Übertrag- {ooo} /([ oooooooooo ]<[ooo/ooo\]>) \ Beförderung- {ooo} /([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>) \ -Übertrag- und 3x -Zusammenfassung- {ooo}/([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito) ([/o\]<[ooo/ooo\]>) \ 3x Distribution von <[ooo/ooo\]> {ooo}/( )( )( ) ([/o\]<[ooo/ooo\]>) \ 3x Inversion von [ooo/ooo\] {ooo}/ooo ([//oooooooooo\\]<[ooo/ooo\]>) \ -Übertrag- {ooo}/ooo //([ oooooooooo ]<[ooo/ooo\]>) \\\ 2x Beförderung- {ooo}/ooo //([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>) \\\ -Übertrag- und 3x -Zusammenfassung- {ooo}/ooo//([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito)([/o\]<[ooo/ooo\]>) \\\ 3x Distribution von <[ooo/ooo\]> {ooo}/ooo//( )( )( )([/o\]<[ooo/ooo\]>) \\\ 3x Inversion von [ooo/ooo\] {ooo}/ooo//ooo ([//oooooooooo\\]<[ooo/ooo\]>) \\\ -Übertrag- {ooo}/ooo//ooo //([ oooooooooo ]<[ooo/ooo\]>)\\\\\ 2x Beförderung- ...
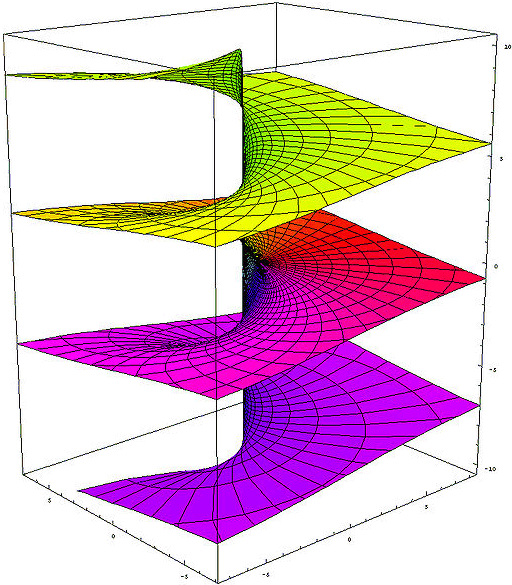
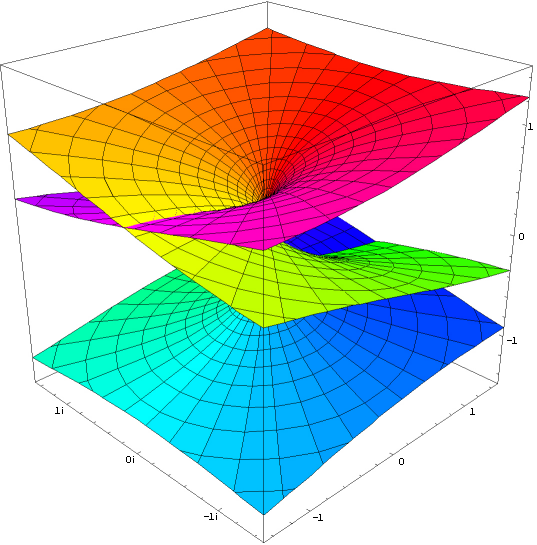
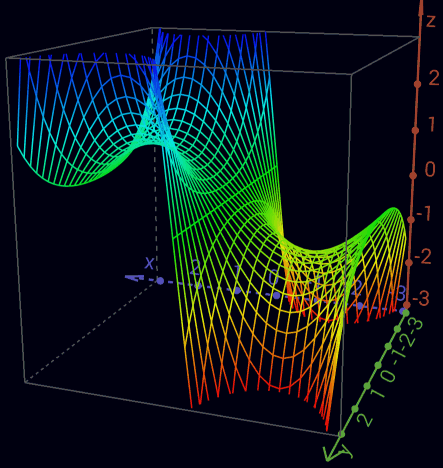
Realteil der komplexen Exponentialfunktion
Imaginärteil der komplexen Exponentialfunktion Transzendental J := [<o>] Phasen-Element Definition J := ln -1 = πi (~3.1415926535i) (J) = ([<o>]) = <o> Abbau2 eJ = eπi = -1 (o) Eulersche Zahl e1 = e (~2.71828182845) ((o)) ee (~15.1542622414) [<(a)>] = a[<o>] Phasenunabhängigkeit von a Theorem 6 ln -ea = a + ln -1 JJ = J-Aufhebung Theorem 7 J = <J> Selbstinversheit von J Theorem 8 i := (([J]<[oo]>)) imaginäre Einheit Definition i := √-1 = eJ/2 i = (<[<i>]>) = <(<[i]>)> imaginäre Einheit Theorem 9 i = 1/-i = -e-ln i ([<J>][i]) = <([J][i])> = ([J][<i>]) = ([J]<[i]>) Kreiszahl Pi π = -J*i = J*-i = J/i (~3.1415926535) (([[<o>]][<i>])) = (([[<o>]]<[i]>)) eπ = (-1)-i = (-1)1/i (~23.1406926328) So wie ln im Imaginären um ein beliebiges Vielfaches von 2π mehrdeutig ist, so werden bei e alle (komplexen) Werte alle 2πi wiederholt. Um dieses abzubilden ist die J-Aufhebung und Selbstinversheit von J nur innerhalb einer Instanzierung zulässig, bzw. sie müssen in insgesamt mindestens einer Instanzierung mehr enthalten sein als in Abstraktionen. Andernfalls wäre ein Widersprüche produzierendes Wuchern von Phasen-Elementen möglich. Beweis der Phasenunabhängigkeit von a [<(a)> ] [<(a)>( [ ])] -Abbau2 [<(a)>(a[ ])] -Null-Kardinalität von (a) [<(a)>(a[o <o>])] -Inversion von o [<(a)>(a[o])(a[<o>])] Distribution von a [<(a)>(a )(a[<o>])] Abbau1 [ (a[<o>])] Inversion von (a) a[<o>] Abbau1 Beweis der J-Aufhebung [<o>][<o>] [<([<o>])>] -Phasenunabhängigkeit von [<o>] [< <o> >] Abbau2 [ o ] Inversionsaufhebung Abbau1 Beweis der Selbstinversheit von J J J< > -Inversion von J<J J> -J-Aufhebung J<J><J> -Inversionszusammenfassung <J> Inversion von J
f1(x) = x2 f2(x) = √x f1(f2(x)) = x (√x)2 = x f2(f1(x)) = ±x √(x2) = ±x
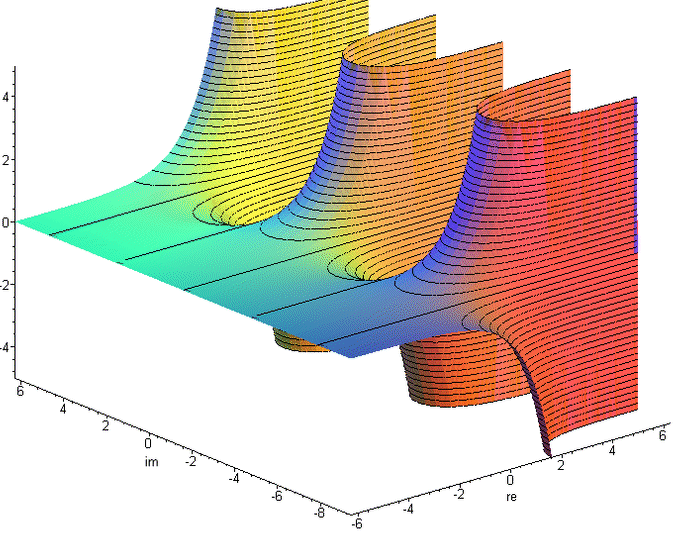
Realteil und Imaginärteil der komplexen Quadratwurzel
Realteil und Imaginärteil der komplexen Kubikwurzel Immer wenn der Exponent eine nichtganze rationale Zahl ist, gibt es eine Mehrdeutigkeit. Die Mehrdeutigkeit ist gleich dem (teilerfremden) Nenner. Wenn der Exponent kleiner 0 ist, ergibt die Basis gleich 0 einen entarteten Punkt. i * i = i2 = -1 ( [(([J]<[oo]>))] [(([J]<[oo]>))] ) (([ [(([J]<[oo]>))] ][oo])) Kardinalität von [(([J]<[oo]>))] (( [J]<[oo]> [oo])) 2x Abbau1 (( [J] )) Inversion von [oo] <o> 2x Abbau2 Beweis der imaginären Einheit <(< [i]> )> <(< [i]><[i] >[i])> Inversion von [i] <(< [i] [i] >[i])> Inversionszusammenfassung <(<[([i] [i])]>[i])> -Abbau1 <(<[ <o> ]>[i])> i * i = -1 <<(<[ o ]>[i])>> Inversionsbeförderung1 ( [i]) Inversionsaufhebung, Abbau1, Inversion von i Abbau2 -1 * -1 = 1 ([<o>][<o>]) ( ) J-Aufhebung ee = ee (([[(o)]][(o)])) (( o )) 3x Abbau1 < a > = ([<([a])>]) = ([a][<o>]) = ([a]J) 2x-Abbau2, Phasenunabhängigkeit von [a] [< a >] = [<([a])>] = [a][<o>] = [a]J -Abbau2, Phasenunabhängigkeit von [a] <( a )> = ([<( a )>]) = ( a [<o>]) = ( a J) -Abbau2, Phasenunabhängigkeit von a Unbestimmtheit der Kardinalität von J innerhalb von () ... = (<JJJJ>) = (<JJ>) = o = (JJ) = (JJJJ) = ... J-Aufhebung, Inversion von ... = (<JJJ>) = (<J>) = (J) = (JJJ) = (JJJJJ) = ... J-Aufhebung, Selbstinversheit von J π * i = J ([ ([<J>][i]) ][i]) ( [<J>][i] [i]) Abbau1 ( [<J>][<o> ]) i * i = -1 <<( [ J ][ o ])>> 2x Inversionsbeförderung1 J Inversionsaufhebung, Abbau1, Abbau2 J/i = π * i / i = π ([ J ]<[i]>) ([([ ([<J>][i]) ][i])]<[i]>) J = π * i ( [<J>][i] [i] <[i]>) 2x Abbau1 ( [<J>][i] ) Inversion von [i] ii = eJ*i/2 = e-π/2 (([[ (([J]<[oo]>)) ]][i])) (( [J]<[oo]> [i])) 2x Abbau1 i-2i = eπ (([[ (([J]<[oo]>)) ]][<i>][oo])) (( [J]<[oo]> [<i>][oo])) 2x Abbau1 (( [J] [<i>] )) Inversion von [oo] 1/√a = √(1/a) (<[(([ [a] ]<[oo]>))]>) (< ([ [a] ]<[oo]>) >) Abbau1 ( ([<[a]>]<[oo]>) ) -Inversionsbeförderung1 √9 = √±32 = ±3 (([[ ooooooooo ]]<[oo]>)) (([[( [ooo][ooo] )]]<[oo]>)) Kardinalität von ooo (([[(([[ooo]][oo]))]]<[oo]>)) Kardinalität von [ooo] (( [[ooo]][oo] <[oo]>)) 2x Abbau1 (( [[ooo]] )) Inversion von [oo] ooo 2x Abbau2 und (([[ ooooooooo ]]<[oo]>)) (([[ ( [ ooo ][ ooo ]) ]]<[oo]>)) Kardinalität von ooo (([[<<( [ ooo ][ ooo ])>>]]<[oo]>)) -Inversionsaufhebung (([[ ( [<ooo>][<ooo>]) ]]<[oo]>)) 2x -Inversionsbeförderung1 (([[ (([[<ooo>]][oo]) ) ]]<[oo]>)) Kardinalität von [<ooo>] (( [[<ooo>]][oo] <[oo]>)) 2x Abbau1 (( [[<ooo>]] )) Inversion von [oo] <ooo> 2x Abbau2 (√3)2 = 3 (([[ (([[ooo]]<[oo]>)) ]][oo])) (( [[ooo]]<[oo]> [oo])) 2x Abbau1 (( [[ooo]] )) Inversion von [oo] ooo 2x Abbau2 -22 = 22 (([[<oo>]][oo])) ([<oo>][<oo>]) -Kardinalität von [<oo>] <<([ oo ][ oo ])>> 2x Inversionsbeförderung1 ([ oo ][ oo ]) Inversionsaufhebung (([[oo]][oo])) Kardinalität von [oo] ab = ((±a2)1/2)b = -ab (( [[ a ]] [b])) (( [[ a ]][oo] <[oo]>[b])) -Inversion von [oo] !!! Zweideutigkeit (([[ (([[ a ]][oo])) ] ]<[oo]>[b])) 2x -Abbau1 (([[ ( [ a ][ a ] ) ] ]<[oo]>[b])) -Kardinalität von [a] (([[<<( [ a ][ a ] )>>] ]<[oo]>[b])) -Inversionsaufhebung (([[ ( [<a>][<a>] ) ] ]<[oo]>[b])) 2x -Inversionsbeförderung1 (([[ (([[<a>]][oo])) ] ]<[oo]>[b])) Kardinalität von [<a>] (( [[<a>]][oo] <[oo]>[b])) 2x Abbau1 (( [[<a>]] [b])) Inversion von [oo]
Dreidimensionale Darstellung der eulerschen Formel ez*i = cos z + i sin z => (([z]([J]<[oo]>)))
Realteil der komplexen Sinusfunktion
Imaginärteil der komplexen Sinusfunktion an+1 = ([an]J) o -> (J) -> o -> (J) -> o -> ... <= (1 -> -1 -> 1 -> -1 -> 1 -> ...) an+1 = ([an][i]) o -> i -> (J) -> <i> -> o -> ... <= (1 -> i -> -1 -> -i -> 1 -> ...) an+1 = <([an][i])> o -> <i> -> (J) -> i -> o -> ... <= (1 -> -i -> -1 -> i -> 1 -> ...) ea*i = cos a + i sin a => (([a][i])) e-a*i = cos a - i sin a => (([<a>][i])) sin a = (ea*i - e-a*i)/2i => ([ (([a][i]))<(([<a>][i]))>]<[oo][i]>) cos a = (ea*i + e-a*i)/2 => ([ (([a][i])) (([<a>][i])) ]<[oo] >) ea = cosh a + sinh a => (a) e-a = cosh a - sinh a => (<a>) sinh a = (ea - e-a)/2 => ([(a)<(<a>)>]<[oo]>) cosh a = (ea + e-a)/2 => ([(a) (<a>) ]<[oo]>) sin(x + i y) = sin(x) cosh(y) + i cos(x) sinh(y) cos(x + i y) = cos(x) cosh(y) - i sin(x) sinh(y) sin(z) = -i sinh(i z) sinh(z) = -i sin(i z) cos(z) = cosh(i z) cosh(z) = cos(i z) sin'(z) = cos(z) sinh'(z) = cosh(z) cos'(z) = -sin(z) cosh'(z) = sinh(z) Einheitskreis x2 + y2 = 1 (([[x]][oo])) (([[y]][oo])) = o Einheitshyperbel x2 - y2 = 1 (([[x]][oo]))<(([[y]][oo]))> = o