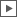Constructive numbers
What I would like to present here as constructive numbers is based on a calculus by Jeffrey M. James, which he had presented in his master thesis "A Calculus of Number Based on Spatial Forms" from 1993. This in turn builds on ideas of John Horton Conway, George Spencer-Brown, Louis H. Kauffman and William Bricken auf. Using only three different brackets, James' calculus generates a very powerful number base with many interesting properties, starting from three simple axioms. It is not practical to do an accounting with the minimalistic notation without any syntactic sugar, but calculation rules and laws are made visible in a vivid and almost meditative way.
The calculus uses three different brackets. A round one for the e-function, a square one for the natural logarithm ln(x) and a angle one for the inversion. The nested tree structures constructed in this way use the drawing background as an empty space, so to speak, which is given a structure by their boundary drawings. Since e0 is equal to 1, if one allows only round brackets for the e-function, and does not allow to nest the brackets, one obtains a calculus for the natural numbers. If one additionally allows angle brackets for the inversion, which may be nested with the round brackets, one obtains the integers. Together with square brackets for the natural logarithm, which may only be nested alternately with the round brackets, whereby there are still no restrictions for the angle brackets, the rational numbers result. One could also describe these as arbitrarily nested multiplications and inversions of integers. If we additionally allow exponentiations with arbitrarily nested bases and rational exponents, we get the algebraic numbers.
If, with the exception of ln(0) with again two restrictions, one releases all nesting possibilities, one obtains an infinite distributive lattice of transcendental field extension, each with countably infinite degree of transcendence.
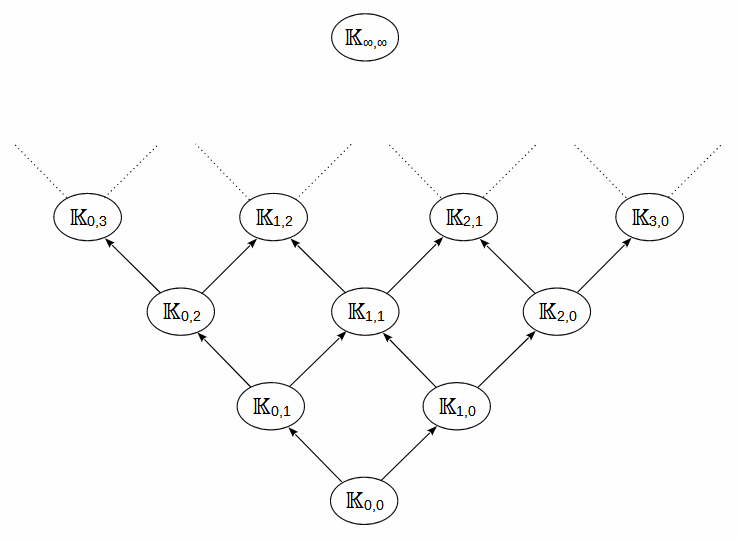
𝕂0,0 = 𝔸
𝕂0,1 = 𝔸({ln k | k ∈ 𝔸\0})
𝕂1,0 = 𝔸({ek | k ∈ 𝔸})
𝕂0,2 = 𝕂0,1({ln k | k ∈ 𝕂0,1\0})
𝕂1,1 = 𝕂0,1({ek | k ∈ 𝕂0,1}) = 𝕂1,0({ln k | k ∈ 𝕂1,0\0})
𝕂2,0 = 𝕂1,0({ek | k ∈ 𝕂1,0})
...
𝕂n,m+1 = 𝕂n,m({ln k | k ∈ 𝕂n,m\0})
𝕂n+1,m = 𝕂n,m({ek | k ∈ 𝕂n,m})
...
𝕂∞,∞
The smallest field of the lattice 𝕂0,0 is equal to the algebraic numbers and the largest is 𝕂∞,∞.
In it, e-functions and natural logarithms can be nested potentially infinitely many times.
e would be element in all fields containing at least 𝕂1,0
and ee in all from 𝕂2,0.
π would be element in all fields containing at least 𝕂0,1,
ln(π) in all from 𝕂0,2
and eπ in all from 𝕂1,1.
However, there is still no proof that e and π are algebraically independent,
even though it looks very much like it.
But even if they were, in the extreme case only the transcendence degrees within the lattice would be smaller.
All fields of the lattice have countably infinite power,
since a simple algorithm could iteratively construct all elements.
Because of this, my suggestion would be to name the number fields as constructive numbers.
Real numbers are overcountably infinite compared to these.
Thus there are real numbers which lie outside of 𝕂∞,∞.
These could be called destructive numbers.
However, it is already difficult to prove the irrationality or transcendence of certain numbers.
Probably, proving the destructiveness of numbers is even more difficult.
The first number for which the proof of its transcendence succeeded in 1844 is a Liouville number.
To my mind, it is a hot candidate for a number that is not only transcendent but even destructive.
f1(x) = x f2(x) = -x f3(x) = ex f4(x) = ln x f3(f4(x)) = x eln x = x f4(f3(x)) = x ln ex = x <> - Inversion -0 = 0 () = o - Instanziation e0 = 1 [] = ∎ - Abstraction ln 0 = -∞ + [-∞...∞]i (complete ambiguity in the imaginary part) [(a)] = ([a]) = a Involution Axiom 1 ln ea = eln a = a (a[bc]) = (a[b])(a[c]) Distribution of a Axiom 2 ea + ln (b + c) = ea + ln b + ea + ln c a<a> = Inversion of a Axiom 3 a - a = 0 <<a>> = a Inverse Cancellation (double Inversion) Theorem 1 -(-a) = a <a><b> = <ab> Inverse Collection Theorem 2 (-a) + (-b) = -(a + b) Proof of Inverse Cancellation for a != ∎ <<a>> <<a>><a>a -Inversion of a a Inversion of <a> Proof of Inverse Collection for a,b != ∎ <a><b> <a><b>ab<ab> -Inversion of ab <ab> Inversion of a and b Proof of additive self-inversion of void (ambiguous sign) -0 = 0 <> Inversion of void Cardinality of a (aggregation second degree) a = ([a]) = ([a][o]) -Involution2, -Involution1 aa = ([a][o])([a][o]) = ([a][oo]) 2x a, -Distribution of [a] a...a = ([a][o...o]) induction step over n ∈ ℕ a * b => ([a][b]) a / b => ([a]<[b]>) for b != Proof of Associativity of multiplication (a*b)*c = a*(b*c) ([([a] [b])][c] ) ( [a] [b] [c] ) Involution1 ( [a][([b] [c])]) -Involution1 Proof of multiplicative self-inversion of o 1/1 = 1 (<[o]>) (< >) Involution1 ( ) Inversion of void
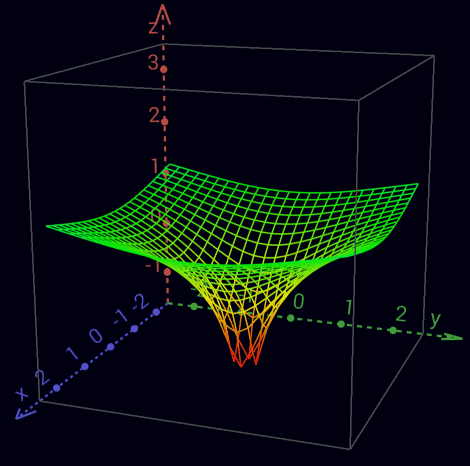
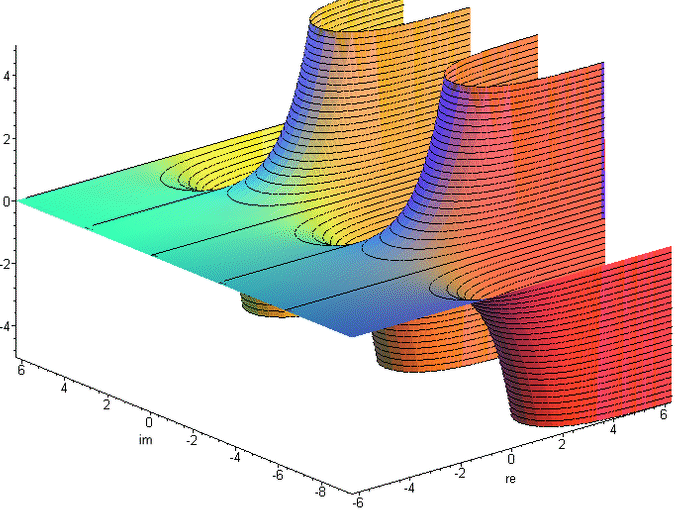
Real part of the complex logarithm
Imaginary part of the complex logarithm - Riemann surface Absorption ([a]∎) = Zero cardinality of a Theorem 3 a * 0 = 0 Proof of Zero cardinality of a ([a]∎) ([a]∎)([a][b])<([a][b])> -Inversion of ([a][b]) ([a][b])<([a][b])> -Distribution of [a] Inversion of ([a][b]) Indefiniteness of cardinality of ∎ within () 0 = eln 0 = 0 * 0 = 0 * 0 * 0 = ... = (∎) = (∎∎) = (∎∎∎) = (∎∎∎∎) = ... -Involution2, -Zero cardinality of void = <> = [o] = (∎) = [(<>)] = ([<>]) = <[o]> = <(∎)> 5x Inversion of void, 3x Involution1, 3x Involution2 Indefiniteness of Inversion of ∎ within () (<∎>) = ([o]<∎>) <= 1/0 is undefined (singularity) 0 * ? = 1 zero don't have multiplicative inverse 0/0 ambiguous 0/a = 0 a/a = 1 a/0 = ∞ Cardinality of [a] (aggregation third degree) ([a]...[a]) = (([[a]][o...o])) (([[a]][b])) ab Due to the complete ambiguity in the imaginary part of ln 0, ∎ is defined besides the zero cardinality only at a 0-basis. 0n = 0 n ∈ ℕ \ 0 (([∎][o...n])) ( ∎...n ) cardinality von ∎ ( ∎ ) Indefiniteness of cardinality von ∎ Involution2 0q = 0 q ∈ ℚ \ 0 (( [∎][ q ])) (( [∎][([m] <[n]>)])) m, n ∈ ℕ \ 0 (( [∎] [m] <[n]> )) Involution1 (([[(([∎] [m]))]]<[n]> )) 2x -Involution1 (([[ ]]<[n]> )) 0m = 0 (( [∎] <[n]> )) Indefiniteness of cardinality von ∎ (( [∎] [(<[n]>)])) -Involution1 Zero cardinality of (<[n]>) 00 = 1 (([∎]∎)) ( ) Zero cardinality of ∎ a0 = 1 (([[a]]∎)) ( ) Zero cardinality of [a] a1 = a (([[a]][o])) (([[a]] )) Involution1 a 2x Involution2 Since multiplication is as commutative as addition, factors can be aggregated just like summands. Addition 2 + 4 = 6 Multiplikation 2 * 4 = 2 + 2 + 2 + 2 = 8 Exponentiation 24 = 2 * 2 * 2 * 2 = 16 Tetration 42 = 2222 = 224 = 216 = 65.536 Hyper-5 24 = 2222 = 422 = 65.5362 = 2...2 65.536 times - therefore, our universe is far too small ... Since exponentiation is not commutative, exponents cannot be represented aggregated like summands or factors. Thus aggregations lose their beauty and thus their usefulness from here on. oo ooo 2 + 3 = 5 ( [oo] [ooo] ) = oo oo oo 2 * 3 = 2 + 2 + 2 = 6 (([[oo]] [ooo])) = ([oo][oo][oo]) 23 = 2 * 2 * 2 = 8 (([[oo]][ (([[oo]][oo])) ])) = (([[oo]][oooo])) 32 = 222 = 24 = 16 (([[oo]][ (([[oo]][ (([[oo]][oo])) ])) ])) 23 = 222 = 42 = 2222 = 65.536 ... 2+2 = 2*2 = 22 = 22 = 22 = ... = 4 Inversion ( [<a>]b ) = <( [a]b )> Inverse Promotion1 Theorem 4 -a * eb = -(a * eb) (<[<a>]b>c) = <(<[a]b>c)> Inverse Promotion2 Theorem 5 1/-a * eb = -(1/a * eb) Proof of Inverse Promotion1 ([<a>]b) <([a]b)>([a]b)([<a>]b) -Inversion of ([a]b) <([a]b)>([a <a>]b) -Distribution von b <([a]b)>([ ]b) Inversion of a <([a]b)>([ ] ) Zero cardinality of (b) <([a]b)> Involution2 Proof of Inverse Promotion2 (c<b [<a>]> ) (c<b [<a>]><[<d>] >[<d>]) -Inversion of [<d>] <(c<b [<a>]><[<d>] >[ d ])> Inverse Promotion1 <(c<b [<a>] [<d>] >[ d ])> Inverse Collection <(c<b[ ([<a>] [<d>]) ]>[ d ])> -Involution1 <(c<b[<<([ a ] [ d ])>>]>[ d ])> 2x Inverse Promotion1 <(c<b[ ([ a ] [ d ]) ]>[ d ])> Inverse Cancellation <(c<b [ a ] [ d ] >[ d ])> Involution1 <(c<b [ a ]><[ d ] >[ d ])> -Inverse Collection <(c<b [ a ]> )> Inversion of [d] Operators -a => <a> a+b => ab a+b+c => abc a-b => a<b> a*b => ([a][b]) a*b*c => ([a][b][c]) a*-b => ([a][<b>]) = <([a][b])> = ([<a>][b]) +-Inverse Promotion1 a/b => ([a]<[b]>) for b != 1/b => ([o]<[b]>) = (<[b]>) Involution1 for b != a/a => ([a]<[a]>) = o Inversion of [a] for a != ab => (([[a]][b])) a1 => (([[a]][o])) = (([[a]])) = a Involution1, 2x Involution2 a-b => (([[a]][<b>])) a1/b => (([[a]]<[b]>)) = (([[a]][(<[b]>)])) -Involution1 for b != ac/b => (([[a]]<[b]>[c])) = (([[a]][(<[b]>[c])])) -Involution1 for b != abc (([[a]][(([[b]][c]))])) (([[a]] ([[b]][c]) )) Involution1 ((ab)c)1/d = ab * c / d (([[(([[(([[a]][b]))]][c]))]]<[d]>)) (( [[a]][b] [c] <[d]>)) 4x Involution1 (1/a)b = a-b ( ([[(<[a]>)]][ b ]) ) ( ([ <[a]> ][ b ]) ) Involution1 (<([ [a] ][ b ])>) Inverse Promotion1 ( ([ [a] ][<b>]) ) -Inverse Promotion1 ab * ac = ab + c ([(([[a]][b]))][(([[a]][c]))]) ( ([[a]][b]) ([[a]][c]) ) 2x Involution1 ( ([[a]][b c]) ) Distribution of [[a]] ac * bc = (a * b)c ([(([[a]][c]))][(([[b]][c]))]) ( ([[a]][c]) ([[b]][c]) ) 2x Involution1 ( ([[a] [b]][c]) ) Distribution of [c] 1 / e = e-1 ([o]<[(o)]>) ( <[(o)]>) ( < o >) 2x Involution1 1 / e2 = e-2 ([o]<[(oo)]>) ( <[(oo)]>) ( < oo >) 2x Involution1 ln (a * b) = ln a + ln b [([a][b])] [a][b] Involution1 ln (a / b) = ln a - ln b [([a]<[b]>)] [a]<[b]> Involution1 ln (ab) = ln a * b [(([[a]][b]))] ([[a]][b]) Involution1 logb a = ln a/ln b ([[a]]<[[b]]>) 1/(1/a) = a (<[(<[a]>)]>) (< <[a]> >) Involution1 ( [a] ) Inverse Cancellation a Involution2 (1/a)*(1/b) = 1/(a*b) ([(< [a]>)][(<[b] >)]) ( < [a]> <[b] > ) 2x Involution1 ( < [a] [b] > ) Inverse Collection ( <[([a] [b])]> ) -Involution1 a/c + b/d = (a*d + b*c) / c*d ( [a] <[c]>)( [b] <[d]>) ( [a][d] <[d]><[c]>)( [b][c] <[c]><[d]>) -Inversion of [d] and [c] ( [a][d] <[d] [c]>)( [b][c] <[c] [d]>) 2x Inverse Collection ([([a][d])]<[d] [c]>)([([b][c])]<[c] [d]>) 2x -Involution1 ([([a][d]) ([b][c])]<[c] [d]>) -Distribution of <[c][d]> 1/a + 1/b = (a + b) / a*b ( <[a]>)( <[b]>) ([b]<[b]><[a]>)([a]<[a]><[b]>) -Inversion of [b] and [a] ([b]<[b] [a]>)([a]<[a] [b]>) 2x Inverse Collection ([ab]<[a][b]>) -Distribution of <[a][b]> (a + b) * (a - b) = a² - b² ([a b][a <b>]) ([a b][a]) ([a b][<b>]) Distribution of [ab] ([a][a])([b][a]) ([a][<b>]) ([b][<b>]) Distribution of [a] and [<b>] ([a][a])([b][a])<([a][ b ])><([b][ b ])> 2x -Inverse Promotion1 ([a][a]) <([b][ b ])> Inversion of ([a][b]) (([[a]][oo])) <(([[b]][oo]))> Cardinality of [a] and [b] Numbers 0 => 1 => o 2 => oo -1 => <o> -2 => <oo> 1/2 => (<[oo]>) 2/3 => ([oo]<[ooo]>) 43 => ([b][oooo])ooo for b = oooooooooo 243 => ([b][([b][oo])oooo])ooo for b = oooooooooo 1243 => ([b][([b][boo])oooo])ooo for b = oooooooooo Arity {a} = ([oooooooooo][a]) Definition of {} oooooooooo{a} = {o a} Carry+ Cardinality of oooooooooo {a}{b} = {ab} Collection+ ([{a}]b) = {([a]b)} Promotion+ {} = Zero cardinality+ 23 * 114 = 2622 ([ {oo}ooo ] [ {{o}o}oooo ]) ([{oo}][{{o}o}oooo]) ([ooo][{{o}o}oooo]) Distribution of [{{o}o}oooo] {([ oo ][{{o}o}oooo])} ([ooo][{{o}o}oooo]) Promotion+ {{{o}o}oooo{{o}o}oooo} {{o}o}oooo{{o}o}oooo{{o}o}oooo 2x -Cardinality of {{o}o}oooo {{{o}o}oooo{{o}o}oooo} {{o}o}{{o}o}{{o}o}oooooooooooo Collection+ of o {{{o}o}oooo{{o}o}oooo} {{o}o}{{o}o}{{o}oo} oo Carry+ {{{o}o} {{o}o} {o}{o}{o} oooooooooooo} oo Collection+ of {o} {{{o}o} {{o}o} {o}{o}{oo} oo} oo Carry+ {{{o} {o} oooooo} oo} oo Collection+ of {{o}} {{{ oo} oooooo} oo} oo Collection+ of {{{o}}} Inverse Arity /a\ = (<[oooooooooo]>[a]) Definition of /\ /oooooooooo a\ = o/a\ Carry- Cardinality of oooooooooo /a\/b\ = /ab\ Collection- ([/a\]b) = /([a]b)\ Promotion- /\ = Zero cardinality- {/a\} = /{a}\ = a Arity Cancellation 12,1 * 1,012 = 12,2452 ([ {o}oo/o\ ] [ o//o/oo\\\ ]) ([{o}][o//o/oo\\\]) ([oo][o//o/oo\\\]) ([/o\][o//o/oo\\\]) 2x Distribution of [o//o/oo\\\] {([ o ][o//o/oo\\\])}([oo][o//o/oo\\\])/([ o ][o//o/oo\\\])\ 2x Promotion ± { o//o/oo\\\ } o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ 3x -Cardinality of o//o/oo\\\ {o}{ //o/oo\\\ } o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ -Collection+ {o} /o/oo\\ o//o/oo\\\o//o/oo\\\ /o//o/oo\\\ \ Arity Cancellation1 {o}oo /o/oo\\ //o/oo\\\ //o/oo\\\ /o//o/oo\\\ \ Collection+ of o {o}oo /oo/oo\ /o/oo\\ /o/oo\\ //o/oo\\\ \ Collection- of /o\ {o}oo /oo/oooo /oo\ /oo\ /o/oo\\\ \ Collection- of //o\\ {o}oo /oo/oooo /ooooo /oo\\\ \ Collection- of ///o\\\ 100 / 3 = 33,3... ([ {{o}} ]<[ooo]>) {([ {o} ]<[ooo]>)} Promotion+ {([oooooooooo]<[ooo]>)} -Carry+ {([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>) ([o]<[ooo]>)} 3x Distribution of <[ooo]> {( )( )( ) ([o]<[ooo]>)} 3x Inversion of [ooo] {ooo} {([o]<[ooo]>)} -Collection+ {ooo} ([{o}]<[ooo]>) -Promotion+ {ooo} ([oooooooooo]<[ooo]>) -Carry+ {ooo}([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>) ([o]<[ooo]>) 3x Distribution of <[ooo]> {ooo}( )( )( ) ([o]<[ooo]>) 3x Inversion of [ooo] {ooo}ooo ([/oooooooooo\]<[ooo]>) -Carry- {ooo}ooo /([ oooooooooo ]<[ooo]>) \ Promotion- {ooo}ooo/([ooo]<[ooo]>)([ooo]<[ooo]>)([ooo]<[ooo]>)([o]<[ooo]>) \ 3x Distribution of <[ooo]> {ooo}ooo/( )( )( )([o]<[ooo]>) \ 3x Inversion of [ooo] {ooo}ooo/ooo ([/oooooooooo\]<[ooo]>) \ -Carry- {ooo}ooo/ooo /([ oooooooooo ]<[ooo]>)\\ Promotion- ... 100 / 3,3 = 30,3030... ([ {{o}} ]<[ooo/ooo\]>) {([ {o} ]<[ooo/ooo\]>)} Promotion+ {([oooooooooo]<[ooo/ooo\]>)} -Carry+ {([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>)} -Carry- and 3x -Collection- {([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito) ([ /o\ ]<[ooo/ooo\]>)} 3x Distribution of <[ooo/ooo\]> {( )( )( ) ([ /o\ ]<[ooo/ooo\]>)} 3x Inversion of [ooo/ooo\] {ooo} {([ /o\ ]<[ooo/ooo\]>)} -Collection+ {ooo} ([{/o\}]<[ooo/ooo\]>) -Promotion+ {ooo} ([ o ]<[ooo/ooo\]>) Arity Cancellation1 {ooo} ([/oooooooooo\]<[ooo/ooo\]>) -Carry- {ooo} /([ oooooooooo ]<[ooo/ooo\]>) \ Promotion- {ooo} /([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>) \ -Carry- and 3x -Collection- {ooo}/([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito) ([/o\]<[ooo/ooo\]>) \ 3x Distribution of <[ooo/ooo\]> {ooo}/( )( )( ) ([/o\]<[ooo/ooo\]>) \ 3x Inversion of [ooo/ooo\] {ooo}/ooo ([//oooooooooo\\]<[ooo/ooo\]>) \ -Carry- {ooo}/ooo //([ oooooooooo ]<[ooo/ooo\]>) \\\ 2x Promotion- {ooo}/ooo //([ooooooooo/ooo\/ooo\/ooo\/o\]<[ooo/ooo\]>) \\\ -Carry- and 3x -Collection- {ooo}/ooo//([ooo/ooo\]<[ooo/ooo\]>)(dito)(dito)([/o\]<[ooo/ooo\]>) \\\ 3x Distribution of <[ooo/ooo\]> {ooo}/ooo//( )( )( )([/o\]<[ooo/ooo\]>) \\\ 3x Inversion of [ooo/ooo\] {ooo}/ooo//ooo ([//oooooooooo\\]<[ooo/ooo\]>) \\\ -Carry- {ooo}/ooo//ooo //([ oooooooooo ]<[ooo/ooo\]>)\\\\\ 2x Promotion- ...
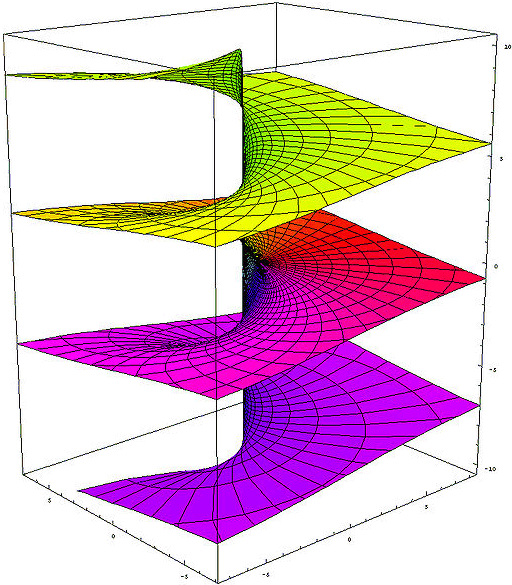
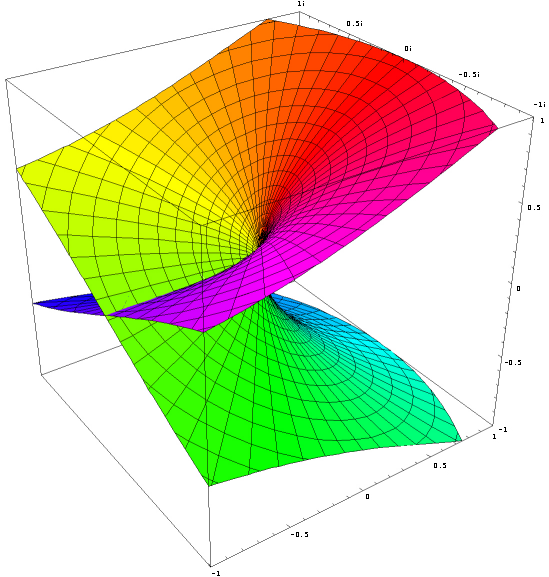
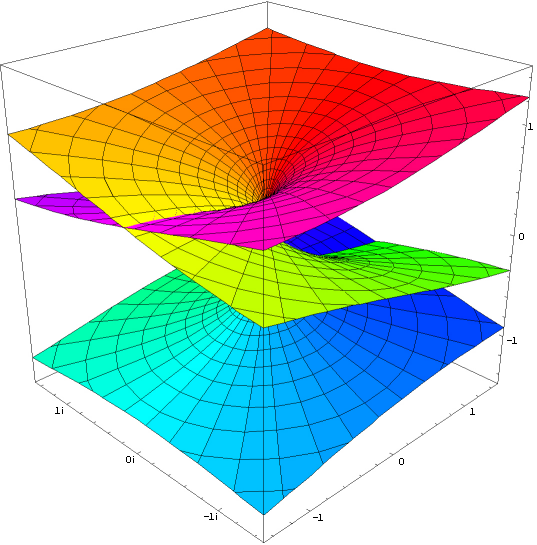
Real part of the complex exponential function
Imaginary part of the complex exponential function Transcendental J := [<o>] Phase Element Definition J := ln -1 = πi (~3.1415926535i) (J) = ([<o>]) = <o> Involution2 eJ = eπi = -1 (o) Euler number e1 = e (~2.71828182845) ((o)) ee (~15.1542622414) [<(a)>] = a[<o>] Phase Independence of a Theorem 6 ln -ea = a + ln -1 JJ = J-cancellation Theorem 7 J = <J> Self-Inversion of J Theorem 8 i := (([J]<[oo]>)) imaginary unit Definition i := √-1 = eJ/2 i = (<[<i>]>) = <(<[i]>)> imaginary unit Theorem 9 i = 1/-i = -e-ln i ([<J>][i]) = <([J][i])> = ([J][<i>]) = ([J]<[i]>) Circle number Pi π = -J*i = J*-i = J/i (~3.1415926535) (([[<o>]][<i>])) = (([[<o>]]<[i]>)) eπ = (-1)-i = (-1)1/i (~23.1406926328) Like ln in the imaginary, by an arbitrary multiple of 2π is ambiguous, so at e all values are repeated every 2πi. To represent this, the J-cancellation and self-inversion of J is permissible only within an instantiation, or they must be contained in at least one more instantiation than in abstractions. Otherwise, a contradiction-producing proliferation of phase elements would be possible. Proof of Phase Independence of a for a != [∎] [<(a)> ] [<(a)>( [ ])] -Involution2 [<(a)>(a[ ])] -Zero cardinality of (a) [<(a)>(a[o <o>])] -Inversion of o [<(a)>(a[o])(a[<o>])] Distribution of a [<(a)>(a )(a[<o>])] Involution1 [ (a[<o>])] Inversion of (a) a[<o>] Involution1 Proof of J-cancellation [<o>][<o>] [<([<o>])>] -Phase Independence von [<o>] [< <o> >] Involution2 [ o ] Inverse Cancellation Involution1 Proof of Self-Inversion of J J J< > -Inversion of void J<J J> -J-cancellation2 J<J><J> -Inverse Collection <J> Inversion of J
f1(x) = x2 f2(x) = √x f1(f2(x)) = x (√x)2 = x f2(f1(x)) = ±x √(x2) = ±x
Real part and imaginary part of the complex square root
Real part and imaginary part of the complex cube root Whenever the exponent is a non-integer rational number, there is an ambiguity. The ambiguity is equal to the (divisor alien) denominator. If the exponent is less than 0, the base equals 0 gives a degenerate point. i * i = i2 = -1 ( [(([J]<[oo]>))] [(([J]<[oo]>))] ) (([ [(([J]<[oo]>))] ][oo])) Cardinality of [(([J]<[oo]>))] (( [J]<[oo]> [oo])) 2x Involution1 (( [J] )) Inversion of [oo] <o> 2x Involution2 Proof of imaginary unit1 <(< [i]> )> <(< [i]><[i] >[i])> Inversion of [i] <(< [i] [i] >[i])> Inverse Collection <(<[([i] [i])]>[i])> -Involution1 <(<[ <o> ]>[i])> i * i = -1 <<(<[ o ]>[i])>> Inverse Promotion1 ( [i]) Inverse Cancellation, Involution1, Inversion of void i Involution2 -1 * -1 = 1 ([<o>][<o>]) ( ) J-cancellation1 ee = ee (([[(o)]][(o)])) (( o )) 3x Involution1 < a > = ([<([a])>]) = ([a][<o>]) = ([a]J) 2x-Involution2, Phase Independence of [a] [< a >] = [<([a])>] = [a][<o>] = [a]J -Involution2, Phase Independence of [a] <( a )> = ([<( a )>]) = (a[<o>]) = (aJ) -Involution2, Phase Independence von a Indefiniteness of Cardinality of J within () ... = (<JJJJ>) = (<JJ>) = o = (JJ) = (JJJJ) = ... J-cancellation, Inversion of void ... = (<JJJ>) = (<J>) = (J) = (JJJ) = (JJJJJ) = ... J-cancellation, Self-Inversion of J π * i = J ([ ([<J>][i]) ][i]) ( [<J>][i] [i]) Involution1 ( [<J>][<o> ]) i * i = -1 <<( [ J ][ o ])>> 2x Inverse Promotion1 J Inverse Cancellation, Involution1, Involution2 J/i = π * i / i = π ([ J ]<[i]>) ([([ ([<J>][i]) ][i])]<[i]>) J = π * i ( [<J>][i] [i] <[i]>) 2x Involution1 ( [<J>][i] ) Inversion of [i] ii = eJ*i/2 = e-π/2 (([[ (([J]<[oo]>)) ]][i])) (( [J]<[oo]> [i])) 2x Involution1 i-2i = eπ (([[ (([J]<[oo]>)) ]][<i>][oo])) (( [J]<[oo]> [<i>][oo])) 2x Involution1 (( [J] [<i>] )) Inversion of [oo] 1/√a = √(1/a) (<[(([ [a] ]<[oo]>))]>) (< ([ [a] ]<[oo]>) >) Involution1 ( ([<[a]>]<[oo]>) ) -Inverse Promotion1 √9 = √±32 = ±3 (([[ ooooooooo ]]<[oo]>)) (([[( [ooo][ooo] )]]<[oo]>)) Cardinality of ooo (([[(([[ooo]][oo]))]]<[oo]>)) Cardinality of [ooo] (( [[ooo]][oo] <[oo]>)) 2x Involution1 (( [[ooo]] )) Inversion of [oo] ooo 2x Involution2 and (([[ ooooooooo ]]<[oo]>)) (([[ ( [ ooo ][ ooo ]) ]]<[oo]>)) Cardinality of ooo (([[<<( [ ooo ][ ooo ])>>]]<[oo]>)) -Inverse Cancellation (([[ ( [<ooo>][<ooo>]) ]]<[oo]>)) 2x -Inverse Promotion1 (([[ (([[<ooo>]][oo]) ) ]]<[oo]>)) Cardinality of [<ooo>] (( [[<ooo>]][oo] <[oo]>)) 2x Involution1 (( [[<ooo>]] )) Inversion of [oo] <ooo> 2x Involution2 (√3)2 = 3 (([[ (([[ooo]]<[oo]>)) ]][oo])) (( [[ooo]]<[oo]> [oo])) 2x Involution1 (( [[ooo]] )) Inversion of [oo] ooo 2x Involution2 -22 = 22 (([[<oo>]][oo])) ([<oo>][<oo>]) -Cardinality of [<oo>] <<([ oo ][ oo ])>> 2x Inverse Promotion1 ([ oo ][ oo ]) Inverse Cancellation (([[oo]][oo])) Cardinality of [oo] ab = ((±a2)1/2)b = -ab (( [[ a ]] [b])) (( [[ a ]][oo] <[oo]>[b])) -Inversion of [oo] !!! Double entendre (([[ (([[ a ]][oo])) ] ]<[oo]>[b])) 2x -Involution1 (([[ ( [ a ][ a ] ) ] ]<[oo]>[b])) -Cardinality of [a] (([[<<( [ a ][ a ] )>>] ]<[oo]>[b])) -Inverse Cancellation (([[ ( [<a>][<a>] ) ] ]<[oo]>[b])) 2x -Inverse Promotion (([[ (([[<a>]][oo])) ] ]<[oo]>[b])) Cardinality of [<a>] (( [[<a>]][oo] <[oo]>[b])) 2x Involution1 (( [[<a>]] [b])) Inversion of [oo]
Three-dimensional representation of the Eulerian formula ez*i = cos z + i sin z => (([z]([J]<[oo]>)))
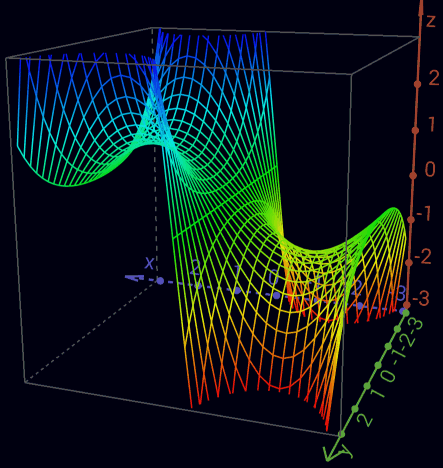
Real part of the complex sine function
Imaginary part of the complex sine function an+1 = ([an]J) o -> (J) -> o -> (J) -> o -> ... <= (1 -> -1 -> 1 -> -1 -> 1 -> ...) an+1 = ([an][i]) o -> i -> (J) -> <i> -> o -> ... <= (1 -> i -> -1 -> -i -> 1 -> ...) an+1 = <([an][i])> o -> <i> -> (J) -> i -> o -> ... <= (1 -> -i -> -1 -> i -> 1 -> ...) ea*i = cos a + i sin a => (([a][i])) e-a*i = cos a - i sin a => (([<a>][i])) sin a = (ea*i - e-a*i)/2i => ([ (([a][i]))<(([<a>][i]))>]<[oo][i]>) cos a = (ea*i + e-a*i)/2 => ([ (([a][i])) (([<a>][i])) ]<[oo] >) ea = cosh a + sinh a => (a) e-a = cosh a - sinh a => (<a>) sinh a = (ea - e-a)/2 => ([(a)<(<a>)>]<[oo]>) cosh a = (ea + e-a)/2 => ([(a) (<a>) ]<[oo]>) sin(x + i y) = sin(x) cosh(y) + i cos(x) sinh(y) cos(x + i y) = cos(x) cosh(y) - i sin(x) sinh(y) sin(z) = -i sinh(i z) sinh(z) = -i sin(i z) cos(z) = cosh(i z) cosh(z) = cos(i z) sin'(z) = cos(z) sinh'(z) = cosh(z) cos'(z) = -sin(z) cosh'(z) = sinh(z) unit circle x2 + y2 = 1 (([[x]][oo])) (([[y]][oo])) = o unit hyperbole x2 - y2 = 1 (([[x]][oo]))<(([[y]][oo]))> = o